Системой m линейных уравнений с n неизвестными называется система вида
где a ij и b i (i =1,…,m ; b =1,…,n ) – некоторые известные числа, а x 1 ,…,x n – неизвестные. В обозначении коэффициентов a ij первый индекс i обозначает номер уравнения, а второй j – номер неизвестного, при котором стоит этот коэффициент.
Коэффициенты при неизвестных будем записывать в виде матрицы 
, которую назовём матрицей
системы
.
Числа, стоящие в правых частях уравнений, b 1 ,…,b m называются свободными членами.
Совокупность n чисел c 1 ,…,c n называется решением данной системы, если каждое уравнение системы обращается в равенство после подстановки в него чисел c 1 ,…,c n вместо соответствующих неизвестных x 1 ,…,x n .
Наша задача будет заключаться в нахождении решений системы. При этом могут возникнуть три ситуации:
Система линейных уравнений, имеющая хотя бы одно решение, называется совместной . В противном случае, т.е. если система не имеет решений, то она называется несовместной .
Рассмотрим способы нахождения решений системы.
МАТРИЧНЫЙ МЕТОД РЕШЕНИЯ СИСТЕМ ЛИНЕЙНЫХ УРАВНЕНИЙ
Матрицы дают возможность кратко записать систему линейных уравнений. Пусть дана система из 3-х уравнений с тремя неизвестными:
Рассмотрим
матрицу системы 
и матрицы столбцы
неизвестных и свободных членов 
Найдем произведение
т.е. в результате произведения мы получаем левые части уравнений данной системы. Тогда пользуясь определением равенства матриц данную систему можно записать в виде
или короче A
∙X=B
.
Здесь матрицы A и B известны, а матрица X неизвестна. Её и нужно найти, т.к. её элементы являются решением данной системы. Это уравнение называют матричным уравнением .
Пусть определитель матрицы отличен от нуля |A | ≠ 0. Тогда матричное уравнение решается следующим образом. Умножим обе части уравнения слева на матрицу A -1 , обратную матрице A : . Поскольку A -1 A = E и E ∙X = X , то получаем решение матричного уравнения в виде X = A -1 B .
Заметим, что поскольку обратную матрицу можно найти только для квадратных матриц, то матричным методом можно решать только те системы, в которых число уравнений совпадает с числом неизвестных . Однако, матричная запись системы возможна и в случае, когда число уравнений не равно числу неизвестных, тогда матрица A не будет квадратной и поэтому нельзя найти решение системы в виде X = A -1 B .
Примеры. Решить системы уравнений.
ПРАВИЛО КРАМЕРА
Рассмотрим систему 3-х линейных уравнений с тремя неизвестными:
Определитель третьего порядка, соответствующий матрице системы, т.е. составленный из коэффициентов при неизвестных,
называется определителем системы .
Составим ещё три определителя следующим образом: заменим в определителе D последовательно 1, 2 и 3 столбцы столбцом свободных членов
Тогда можно доказать следующий результат.
Теорема (правило Крамера). Если определитель системы Δ ≠ 0, то рассматриваемая система имеет одно и только одно решение, причём
Доказательство . Итак, рассмотрим систему 3-х уравнений с тремя неизвестными. Умножим 1-ое уравнение системы на алгебраическое дополнение A 11 элемента a 11 , 2-ое уравнение – на A 21 и 3-е – на A 31 :
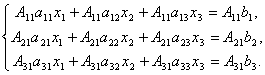
Сложим эти уравнения:
Рассмотрим каждую из скобок и правую часть этого уравнения. По теореме о разложении определителя по элементам 1-го столбца
Аналогично можно показать, что и .
Наконец несложно заметить, что 
Таким образом, получаем равенство: .
Следовательно, .
Аналогично выводятся равенства и , откуда и следует утверждение теоремы.
Таким образом, заметим, что если определитель системы Δ ≠ 0, то система имеет единственное решение и обратно. Если же определитель системы равен нулю, то система либо имеет бесконечное множество решений, либо не имеет решений, т.е. несовместна.
Примеры. Решить систему уравнений
МЕТОД ГАУССА
Ранее рассмотренные методы можно применять при решении только тех систем, в которых число уравнений совпадает с числом неизвестных, причём определитель системы должен быть отличен от нуля. Метод Гаусса является более универсальным и пригоден для систем с любым числом уравнений. Он заключается в последовательном исключении неизвестных из уравнений системы.
Вновь рассмотрим систему из трёх уравнений с тремя неизвестными:
.
Первое уравнение оставим без изменения, а из 2-го и 3-го исключим слагаемые, содержащие x 1 . Для этого второе уравнение разделим на а 21 и умножим на –а 11 , а затем сложим с 1-ым уравнением. Аналогично третье уравнение разделим на а 31 и умножим на –а 11 , а затем сложим с первым. В результате исходная система примет вид:
Теперь из последнего уравнения исключим слагаемое, содержащее x 2 . Для этого третье уравнение разделим на , умножим на и сложим со вторым. Тогда будем иметь систему уравнений:
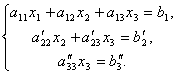
Отсюда из последнего уравнения легко найти x 3 , затем из 2-го уравнения x 2 и, наконец, из 1-го – x 1 .
При использовании метода Гаусса уравнения при необходимости можно менять местами.
Часто вместо того, чтобы писать новую систему уравнений, ограничиваются тем, что выписывают расширенную матрицу системы:
и затем приводят её к треугольному или диагональному виду с помощью элементарных преобразований.
К элементарным преобразованиям матрицы относятся следующие преобразования:
Примеры: Решить системы уравнений методом Гаусса.
Таким образом, система имеет бесконечное множество решений.
Метод Гаусса, называемый также методом последовательного исключения неизвестных, состоит в следующем. При помощи элементарных преобразований систему линейных уравнений приводят к такому виду, чтобы её матрица из коэффициентов оказалась трапециевидной (то же самое, что треугольной или ступенчатой) или близкой к трапециевидной (прямой ход метода Гаусса, далее - просто прямой ход). Пример такой системы и её решения - на рисунке сверху.
В такой системе последнее уравнение содержит только одну переменную и её значение можно однозначно найти. Затем значение этой переменной подставляют в предыдущее уравнение (обратный ход метода Гаусса , далее - просто обратный ход), из которого находят предыдущую переменную, и так далее.
В трапециевидной (треугольной) системе, как видим, третье уравнение уже не содержит переменных y и x , а второе уравнение - переменной x .
После того, как матрица системы приняла трапециевидную форму, уже не представляет труда разобраться в вопросе о совместности системы, определить число решений и найти сами решения.
Чтобы все прониклись простотой, с которой решаются трапециевидные (треугольные, ступенчатые) системы линейных уравнений, приведём решение такой системы с применением обратного хода. Быстрое решение этой системы было показано на картинке в начале урока.
Пример 1. Решить систему линейных уравнений, применяя обратный ход:
Решение. В данной трапециевидной системе переменная z однозначно находится из третьего уравнения. Подставляем её значение во второе уравнение и получаем значение переменой y :
Теперь нам известны значения уже двух переменных - z и y . Подставляем их в первое уравнение и получаем значение переменной x :
Из предыдущих шагов выписываем решение системы уравнений:
Чтобы получить такую трапециевидную систему линейных уравнений, которую мы решили очень просто, требуется применять прямой ход, связанный с элементарными преобразованиями системы линейных уравнений. Это также не очень сложно.
Повторяя школьный метод алгебраического сложения уравнений системы, мы выяснили, что к одному из уравнений системы можно прибавлять другое уравнение системы, причём каждое из уравнений может быть умножено на некоторые числа. В результате получаем систему линейных уравнений, эквивалентную данной. В ней уже одно уравнение содержало только одну переменную, подставляя значение которой в другие уравнений, мы приходим к решению. Такое сложение - один из видов элементарного преобразования системы. При использовании метода Гаусса можем пользоваться несколькими видами преобразований.
На анимации выше показано, как система уравнений постепенно превращается в трапециевидную. То есть такую, которую вы видели на самой первой анимации и сами убедились в том, что из неё просто найти значения всех неизвестных. О том, как выполнить такое превращение и, конечно, примеры, пойдёт речь далее.
При решении систем линейных уравнений с любым числом уравнений и неизвестных в системе уравнений и в расширенной матрице системы можно :
В результате преобразований получаем систему линейных уравнений, эквивалентную данной.
Рассмотрим сначала решение систем линейных уравений, в которых число неизвестных равно числу уравнений. Матрица такой системы - квадратная, то есть в ней число строк равно числу столбцов.
Пример 2. Решить методом Гаусса систему линейных уравнений
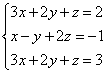
Решая системы линейных уравнений школьными способами, мы почленно умножали одно из уравнений на некоторое число, так, чтобы коэффициенты при первой переменной в двух уравнениях были противоположными числами. При сложении уравнений происходит исключение этой переменной. Аналогично действует и метод Гаусса.
Для упрощения внешнего вида решения составим расширенную матрицу системы :
В этой матрице слева до вертикальной черты расположены коэффициенты при неизвестных, а справа после вертикальной черты - свободные члены.
Для удобства деления коэффициентов при переменных (чтобы получить деление на единицу) переставим местами первую и вторую строки матрицы системы . Получим систему, эквивалентную данной, так как в системе линейных уравнений можно переставлять местами уравнения:
С помощью нового первого уравнения исключим переменную x из второго и всех последующих уравнений . Для этого ко второй строке матрицы прибавим первую строку, умноженную на (в нашем случае на ), к третьей строке – первую строку, умноженную на (в нашем случае на ).
Это возможно, так как
Если бы в нашей системе уравнений было больше трёх, то следовало бы прибавлять и ко всем последующим уравнениям первую строку, умноженную на отношение соответствующих коэффициентов, взятых со знаком минус.
В результате получим матрицу эквивалентную данной системе новой системы уравнений, в которой все уравнения, начиная со второго не содержат переменнную x :
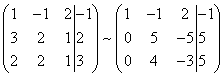
Для упрощения второй строки полученной системы умножим её на и получим вновь матрицу системы уравнений, эквивалентной данной системе:
Теперь, сохраняя первое уравнение полученной системы без изменений, с помощью второго уравнения исключаем переменную y из всех последующих уравнений. Для этого к третьей строке матрицы системы прибавим вторую строку, умноженную на (в нашем случае на ).
Если бы в нашей системе уравнений было больше трёх, то следовало бы прибавлять и ко всем последующим уравнениям вторую строку, умноженную на отношение соответствующих коэффициентов, взятых со знаком минус.
В результате вновь получим матрицу системы, эквивалентной данной системе линейных уравнений:
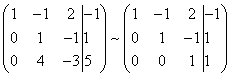
Мы получили эквивалентную данной трапециевидную систему линейных уравнений:
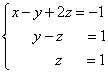
Если число уравнений и переменных больше, чем в нашем примере, то процесс последовательного исключения переменных продолжается до тех пор, пока матрица системы не станет трапециевидной, как в нашем демо-примере.
Решение найдём "с конца" - обратный ход
. Для этого из последнего уравнения определим z
:
.
Подставив это значение в предшествующее уравнение, найдём y
:
Из первого уравнения найдём x
:
Ответ: решение данной системы уравнений - 
.
: в этом случае будет выдан тот же ответ, если система имеет однозначное решение. Если же система имеет бесконечное множество решений, то таков будет и ответ, и это уже предмет пятой части этого урока.
Перед нами вновь пример совместной и определённой системы линейных уравнений, в которой число уравнений равно числу неизвестных. Отличие от нашего демо-примера из алгоритма - здесь уже четыре уравнения и четыре неизвестных.
Пример 4. Решить систему линейных уравнений методом Гаусса:
Теперь нужно с помощью второго уравнения исключить переменную из последующих уравнений. Проведём подготовительные работы. Чтобы было удобнее с отношением коэффициентов, нужно получить единицу в во втором столбце второй строки. Для этого из второй строки вычтем третью, а полученную в результате вторую строку умножим на -1.
Проведём теперь собственно исключение переменной из третьего и четвёртого уравнений. Для этого к третьей строке прибавим вторую, умноженную на , а к четвёртой - вторую, умноженную на .
Теперь с помощью третьего уравнения исключим переменную из четвёртого уравнения. Для этого к четвёртой строке прибавим третью, умноженную на . Получаем расширенную матрицу трапециевидной формы.
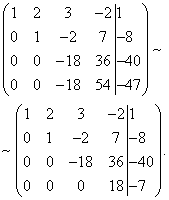
Получили систему уравнений, которой эквивалентна заданная система:
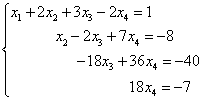
Следовательно, полученная и данная системы являются совместными и определёнными. Окончательное решение находим «с конца». Из четвёртого уравнения непосредственно можем выразить значение переменной "икс четвёртое":
Это значение подставляем в третье уравнение системы и получаем
,
,
Наконец, подстановка значений
В первое уравнение даёт
,
откуда находим "икс первое":
Ответ: данная система уравнений имеет единственное решение 
.
Проверить решение системы можно и на калькуляторе, решающем методом Крамера : в этом случае будет выдан тот же ответ, если система имеет однозначное решение.
Системы линейных уравнений применяются для моделирования реальных объектов физического мира. Решим одну из таких задач - на сплавы. Аналогичные задачи - задачи на смеси, стоимость или удельный вес отдельных товаров в группе товаров и тому подобные.
Пример 5. Три куска сплава имеют общую массу 150 кг. Первый сплав содержит 60% меди, второй - 30%, третий - 10%. При этом во втором и третьем сплавах вместе взятых меди на 28,4 кг меньше, чем в первом сплаве, а в третьем сплаве меди на 6,2 кг меньше, чем во втором. Найти массу каждого куска сплава.
Решение. Составляем систему линейных уравнений:
Умножаем второе и третье уравнения на 10, получаем эквивалентную систему линейных уравнений:
Составляем расширенную матрицу системы:
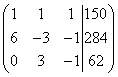
Внимание, прямой ход. Путём сложения (в нашем случае - вычитания) одной строки, умноженной на число (применяем два раза) с расширенной матрицей системы происходят следующие преобразования:
Прямой ход завершился. Получили расширенную матрицу трапециевидной формы.
Применяем обратный ход. Находим решение с конца. Видим, что .
Из второго уравнения находим
Из третьего уравнения -
Проверить решение системы можно и на калькуляторе, решающем методом Крамера : в этом случае будет выдан то же ответ, если система имеет однозначное решение.
О простоте метода Гаусса говорит хотя бы тот факт, что немецкому математику Карлу Фридриху Гауссу на его изобретение потребовалось лишь 15 минут. Кроме метода его имени из творчества Гаусса известно изречение "Не следует смешивать то, что нам кажется невероятным и неестественным, с абсолютно невозможным" - своего рода краткая инструкция по совершению открытий.
Во многих прикладных задачах может и не быть третьего ограничения, то есть, третьего уравнения, тогда приходится решать методом Гаусса систему двух уравнений с тремя неизвестными, или же, наоборот - неизвестных меньше, чем уравнений. К решению таких систем уравнений мы сейчас и приступим.
С помощью метода Гаусса можно установить, совместна или несовместна любая система n линейных уравнений с n переменными.
Следующий пример - совместная, но неопределённая система линейных уравнений, то есть имеющая бесконечное множество решений.
После выполнения преобразований в расширенной матрице системы (перестановки строк, умножения и деления строк на некоторое число, прибавлению к одной строке другой) могли появиться строки вида
Если во всех уравнениях имеющих вид
Свободные члены равны нулю, то это означает, что система неопределённа, то есть имеет бесконечное множество решений, а уравнения этого вида – «лишние» и их исключаем из системы.
Пример 6.
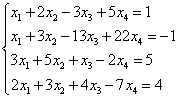
Решение. Составим расширенную матрицу системы. Затем с помощью первого уравнения исключим переменную из последующих уравнений. Для этого ко второй, третьей и четвёртой строкам прибавим первую, умноженную соответственно на :
Теперь вторую строку прибавим к третьей и четвёртой.
В результате приходим к системе
Последние два уравнения превратились в уравнения вида . Эти уравнения удовлетворяются при любых значениях неизвестных и их можно отбросить.
Чтобы удовлетворить второму уравнению, мы можем для и
выбрать произвольные значения
, тогда значение для
определится уже однозначно: 
. Из первого уравнения
значение для также находится
однозначно: 
.
Как заданная, так и последняя системы совместны, но неопределённы, и формулы
при произвольных и дают нам все решения заданной системы.
Следующий пример - несовместная система линейных уравнений, то есть не имеющая решений. Ответ на такие задачи так и формулируется: система не имеет решений.
Как уже говорилось в связи с первым примером, после выполнения преобразований в расширенной матрице системы могли появиться строки вида
соответствующие уравнению вида
Если среди них есть хотя бы одно уравнение с отличным от нуля свободным членом (т.е. ), то данная система уравнений является несовместной, то есть не имеет решений и на этом её решение закончено.
Пример 7. Решить методом Гаусса систему линейных уравнений:
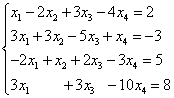
Решение. Составляем расширенную матрицу системы. С помощью первого уравнения исключаем из последующих уравнений переменную . Для этого ко второй строке прибавляем первую, умноженную на , к третьей строке - первую, умноженную на , к четвёртой - первую, умноженную на .
Теперь нужно с помощью второго уравнения исключить переменную из последующих уравнений. Чтобы получить целые отношения коэффициентов, поменяем местами вторую и третью строки расширенной матрицы системы.
Для исключения из третьего и четвёртого уравнения к третьей строке прибавим вторую, умноженную на , а к четвёртой - вторую, умноженную на .
Теперь с помощью третьего уравнения исключим переменную из четвёртого уравнения. Для этого к четвёртой строке прибавим третью, умноженную на .
Заданная система эквивалентна, таким образом, следующей:
Полученная система несовместна, так как её последнее уравнение не может быть удовлетворено никакими значениями неизвестных. Следовательно, данная система не имеет решений.
СИСТЕМЫ ЛИНЕЙНЫХ УРАВНЕНИЙ
I. Постановка задачи.
II. Совместность однородных и неоднородных систем.
III. Система т уравнений с т неизвестными. Правило Крамера.
IV. Матричный метод решения систем уравнений.
V. Метод Гаусса.
I. Постановка задачи.
называют системой
m
линейных уравнений с n
неизвестными
.
Коэффициенты уравнений этой системы
записывают в виде матрицы
которую называют матрицей системы (1).
Числа, стоящие в правых частях уравнений, образуют столбец свободных членов {B }:
.
Если столбец {B }={0 }, то система уравнений называется однородной . В противном случае, когда {B }≠{0 } – система неоднородна .
Система линейных уравнений (1) может быть записана в матричном виде
[A ]{x }={B }. (2)
Здесь
- столбец неизвестных.
Решить систему
уравнений (1) - значит найти совокупность
n
чисел
такую, что при подстановке в систему
(1) вместо неизвестных
каждое уравнение системы обращается в
тождество. Числа
называются решением системы уравнений.
,
может иметь бесчисленное множество решений
или не иметь решений совсем
.
Системы уравнений, не имеющие решений, называются несовместными . Если система уравнений имеет хотя бы одно решение, то она называетсясовместной . Система уравнений называетсяопределенной , если она имеет единственное решение, инеопределенной , если имеет бесчисленное множество решений.
II. Совместность однородных и неоднородных систем.
Условие совместности
системы линейных уравнений (1) формулируется
в теореме
Кронекера-Капелли
:
система линейных уравнений имеет хотя
бы одно решение в том и только в том
случае, когда ранг матрицы системы равен
рангу расширенной матрицы:
.
Расширенной матрицей системы называют матрицу, получающуюся из матрицы системы приписыванием к ней справа столбца свободных членов:
.
Если RgA
Однородные системы
линейных уравнений в соответствии с
теоремой Кронекера-Капелли всегда
совместны. Рассмотрим случай однородной
системы, в которой число уравнений равно
числу неизвестных, то есть т=п
.
Если определитель матрицы такой системы
не равен нулю, т.е.
,
однородная система имеет единственное
решение, которое является тривиальным
(нулевым). Однородные системы имеют
бесчисленное множество решений, если
среди уравнений системы есть линейно
зависимые, т.е.
.
Пример. Рассмотрим однородную систему трех линейных уравнений с тремя неизвестными:
и исследуем вопрос о количестве ее решений. Каждое из уравнений можно считать уравнением плоскости, проходящей через начало координат (D =0 ). Система уравнений имеет единственное решение, когда все три плоскости пересекаются в одной точке. При этом их нормальные векторы некомпланарны, и, следовательно, выполняется условие
.
Решение системы при этом x =0, y =0, z =0 .
Если хотя бы две из трех плоскостей, например, первая и вторая, параллельны, т.е. , то определитель матрицы системы равен нулю, а система имеет бесчисленное множество решений. Причем решениями будут координатыx , y , z всех точек, лежащих на прямой
Если же все три плоскости совпадают, то система уравнений сведется к одному уравнению
,
а решением будут координаты всех точек, лежащих в этой плоскости.
При исследовании неоднородных систем линейных уравнений вопрос о совместности решается с помощью теоремы Кронекера-Капелли. Если же число уравнений в такой системе равно числу неизвестных, то система имеет единственное решение, если ее определитель не равен нулю. В противном случае система либо несовместна, либо имеет бесчисленное множество решений.
Пример . Исследуем неоднородную систему двух уравнений с двумя неизвестными
.
,
.
В этом случае ранг матрицы системы равен
1:RgA
=1
, т.к.
,
а ранг расширенной
матрицы
равен двум, т. к. для нее в качестве
базисного минора может быть выбран
минор второго порядка, содержащий третий
столбец.
В рассматриваемом
случае RgA
Если прямые
совпадают, т.е.
,
то система уравнений имеет бесчисленное
множество решений: координаты точек на
прямой
.
В этом случаеRgA
=
RgA
*
=1.
Система имеет
единственное решение, когда прямые не
параллельны, т.е.
.
Решением этой системы являются координаты
точки пересечения прямых
III. Система т уравнений с т неизвестными. Правило Крамера.
Рассмотрим простейший случай, когда число уравнений системы равно числу неизвестных, т.е. m = n . Если детерминант матрицы системы отличен от нуля, решение системы может быть найдено по правилу Крамера:
(3)
Здесь
- определитель матрицы системы,
- определитель
матрицы, получаемой из [A
]
заменой i
-ого
столбца на столбец свободных
членов:
.
Пример . Решить систему уравнений методом Крамера.
Решение :
1) найдем определитель системы
2) найдем вспомогательные определители
3) найдем решение системы по правилу Крамера:
Результат решения может быть проверен подстановкой в систему уравнений
Получены верные тождества.
IV. Матричный метод решения систем уравнений.
[A ]{x }={B }
и умножим правую и левую части соотношения (2) слева на матрицу [A -1 ], обратную матрице системы:
[A -1 ][A ]{x }=[A -1 ]{B }. (2)
По определению обратной матрицы произведение [A -1 ][A ]=[E ], а по свойствам единичной матрицы [E ]{x }={x }. Тогда из соотношения (2") получаем
{x }=[A -1 ]{B }. (4)
Соотношение (4) лежит в основе матричного метода решения систем линейных уравнений: необходимо найти матрицу, обратную матрице системы, и умножить на нее слева вектор-столбец правых частей системы.
Пример . Решим матричным методом систему уравнений, рассмотренную в предыдущем примере.
Матрица системы
ее определитель detA
==183
.
.Чтобы найти матрицу [A -1 ], найдем матрицу, присоединенную к [A ]:
или
В формулу для
вычисления обратной матрицы входит
,
тогда
Теперь можно найти решение системы
Тогда окончательно
получаем
.
V. Метод Гаусса.
При большом числе неизвестных решение системы уравнений методом Крамера или матричным методом связано с вычислением определителей высокого порядка или обращением матриц больших размеров. Эти процедуры весьма трудоемки даже для современных ЭВМ. Поэтому для решения систем большого числа уравнений чаще пользуются методом Гаусса.
Метод Гаусса заключается в последовательном исключении неизвестных путем элементарных преобразований расширенной матрицы системы. К элементарным преобразованиям матрицы относят перестановку строк, сложение строк, умножение строк на числа, отличные от нуля. В результате преобразований удается матрицу системы свести к верхней треугольной, на главной диагонали которой стоят единицы, а ниже главной диагонали - нули. В этом заключается прямой ход метода Гаусса. Обратный ход метода состоит в непосредственном определении неизвестных, начиная с последнего.
Проиллюстрируем метод Гаусса на примере решения системы уравнений
На первом шаге
прямого хода добиваются того, чтобы
коэффициент
преобразованной системы стал равен
1
,
а коэффициенты
и
обратились в ноль. Для этого первое
уравнение умножим на1/10
,
второе уравнение умножим на 10
и сложим с первым, третье уравнение
умножим на -10/2
и сложим с первым. После этих преобразований
получим
На втором шаге
добиваемся того, чтобы после преобразований
коэффициент
стал равным1
,
а коэффициент
.
Для этого второе уравнение разделим на
42
,
а третье уравнение умножим на -42/27
и сложим со
вторым. Получим систему уравнений
На третьем шаге
должны получить коэффициент
.
Для этого третье уравнение разделим на(37 - 84/27)
;
получим
На этом прямой ход метода Гаусса заканчивается, т.к. матрица системы сведена к верхней треугольной:
Решение
выполняем с помощью калькулятора . Выпишем расширенную и основную матрицы:
Пунктиром отделена основная матрица A. Сверху пишем неизвестные системы, имея в виду возможную перестановку слагаемых в уравнениях системы. Определяя ранг расширенной матрицы, одновременно найдем ранг и основной. В матрице B первый и второй столбцы пропорциональны. Из двух пропорциональных столбцов в базисный минор может попасть только один, поэтому перенесем, например, первый столбец за пунктирную черту с обратным знаком. Для системы это означает перенос членов с x 1 в правую часть уравнений.
Приведем матрицу к треугольному виду. Будем работать только со строками, так как умножение строки матрицы на число, отличное от нуля, и прибавление к другой строке для системы означает умножение уравнения на это же число и сложение с другим уравнением, что не меняет решения системы. Работаем с первой строкой: умножим первую строку матрицы на (-3) и прибавим ко второй и третьей строкам по очереди. Затем первую строку умножим на (-2) и прибавим к четвертой.
Вторая и третья строки пропорциональны, следовательно, одну из них, например вторую, можно вычеркнуть. Это равносильно вычеркиванию второго уравнения системы, так как оно является следствием третьего.
Теперь работаем со второй строкой: умножим ее на (-1) и прибавим к третьей.
Минор, обведенный пунктиром, имеет наивысший порядок (из возможных миноров) и отличен от нуля (он равен произведению элементов, стоящих на главной диагонали), причем этот минор принадлежит как основной матрице, так и расширенной, следовательно rangA = rangB = 3 .
Минор 
является базисным. В него вошли коэффициенты при неизвестных x 2 , x 3 , x 4 , значит, неизвестные x 2 , x 3 , x 4 – зависимые, а x 1 , x 5 – свободные.
Преобразуем матрицу, оставляя слева только базисный минор (что соответствует пункту 4 приведенного выше алгоритма решения).
Система с коэффициентами этой матрицы эквивалентна исходной системе и имеет вид
Методом исключения неизвестных находим:
, ,
Получили соотношения, выражающие зависимые переменные x 2 , x 3 , x 4 через свободные x 1 и x 5 , то есть нашли общее решение:
Придавая свободным неизвестным любые значения, получим сколько угодно частных решений. Найдем два частных решения:
1) пусть x 1 = x 5 = 0, тогда x 2 = 1, x 3 = -3, x 4 = 3;
2) положим x 1 = 1, x 5 = -1, тогда x 2 = 4, x 3 = -7, x 4 = 7.
Таким образом, нашли два решения: (0,1,-3,3,0) – одно решение, (1,4,-7,7,-1) – другое решение.
Пример 2
. Исследовать совместность, найти общее и одно частное решение системы
Решение
. Переставим первое и второе уравнения, чтобы иметь единицу в первом уравнении и запишем матрицу B.
Получим нули в четвертом столбце, оперируя первой строкой:
Теперь получим нули в третьем столбце с помощью второй строки:
Третья и четвертая строки пропорциональны, поэтому одну из них можно вычеркнуть, не меняя ранга:
Третью строку умножим на (–2) и прибавим к четвертой:
Видим, что ранги основной и расширенной матриц равны 4, причем ранг совпадает с числом неизвестных, следовательно, система имеет единственное решение:
;
x 4 = 10- 3x 1 – 3x 2 – 2x 3 = 11.
Пример 3
. Исследовать систему на совместность и найти решение, если оно существует.
Решение
. Составляем расширенную матрицу системы.
Переставляем первые два уравнения, чтобы в левом верхнем углу была 1:
Умножая первую строку на (-1), складываем ее с третьей:
Умножим вторую строку на (-2) и прибавим к третьей:
Система несовместна, так как в основной матрице получили строку, состоящую из нулей, которая вычеркивается при нахождении ранга, а в расширенной матрице последняя строка останется, то есть r B > r A .
Задание
. Исследовать данную систему уравнений на совместность и решить ее средствами матричного исчисления .
Решение
Пример
. Доказать совместимость системы линейных уравнений и решить ее двумя способами: 1) методом Гаусса ; 2) методом Крамера . (ответ ввести в виде: x1,x2,x3)
Решение :doc :doc :xls
Ответ:
2,-1,3.
Пример
. Дана система линейных уравнений. Доказать ее совместность. Найти общее решение системы и одно частное решение.
Решение
Ответ:
x 3 = - 1 + x 4 + x 5 ; x 2 = 1 - x 4 ; x 1 = 2 + x 4 - 3x 5
Задание
. Найти общее и частное решения каждой системы.
Решение.
Исследуем эту систему по теореме Кронекера-Капелли.
Выпишем расширенную и основную матрицы:
| 1 | 1 | 14 | 0 | 2 | 0 |
| 3 | 4 | 2 | 3 | 0 | 1 |
| 2 | 3 | -3 | 3 | -2 | 1 |
| x 1 | x 2 | x 3 | x 4 | x 5 |
| 0 | -1 | 40 | -3 | 6 | -1 |
| 3 | 4 | 2 | 3 | 0 | 1 |
| 2 | 3 | -3 | 3 | -2 | 1 |
| 0 | -1 | 40 | -3 | 6 | -1 |
| 0 | -1 | 13 | -3 | 6 | -1 |
| 2 | 3 | -3 | 3 | -2 | 1 |
| 0 | 0 | 27 | 0 | 0 | 0 |
| 0 | -1 | 13 | -3 | 6 | -1 |
| 2 | 3 | -3 | 3 | -2 | 1 |
| 0 | 0 | 27 | 0 | 0 | 0 |
| 0 | -1 | 13 | -1 | 3 | -6 |
| 2 | 3 | -3 | 1 | -3 | 2 |
| x 1 | x 2 | x 3 | x 4 | x 5 |
Задание
. Решить систему уравнений.
Ответ
:x 2 = 2 - 1.67x 3 + 0.67x 4
x 1 = 5 - 3.67x 3 + 0.67x 4
Придавая свободным неизвестным любые значения, получим сколько угодно частных решений. Система является неопределенной
У школьника имеется 200 рублей, чтобы пообедать в школе. Пирожное стоит 25 рублей, а чашка кофе 10 рублей. Сколько пирожных и чашек кофе можно накупить на 200 рублей?
Обозначим количество пирожных через x , а количество чашек кофе через y . Тогда стоимость пирожных будет обозначаться через выражение 25x , а стоимость чашек кофе через 10y .
25x —
стоимость x
пирожных
10y —
стоимость y
чашек кофе
Итоговая сумма должна равняться 200 рублей. Тогда получится уравнение с двумя переменными x и y
25x + 10y = 200
Сколько корней имеет данное уравнение?
Всё зависит от аппетита школьника. Если он купит 6 пирожных и 5 чашек кофе, то корнями уравнения будут числа 6 и 5.
Говорят, что пара значений 6 и 5 являются корнями уравнения 25x + 10y = 200 . Записывается как (6; 5) , при этом первое число является значением переменной x , а второе — значением переменной y .
6 и 5 не единственные корни, которые обращают уравнение 25x + 10y = 200 в тождество. При желании на те же 200 рублей школьник может купить 4 пирожных и 10 чашек кофе:
В этом случае корнями уравнения 25x + 10y = 200 является пара значений (4; 10) .
Более того, школьник может вообще не покупать кофе, а купить пирожные на все 200 рублей. Тогда корнями уравнения 25x + 10y = 200 будут значения 8 и 0
Или наоборот, не покупать пирожные, а купить кофе на все 200 рублей. Тогда корнями уравнения 25x + 10y = 200 будут значения 0 и 20
Попробуем перечислить все возможные корни уравнения 25x + 10y = 200 . Условимся, что значения x и y принадлежат множеству целых чисел. И пусть эти значения будут бóльшими или равными нулю:
x
∈ Z, y
∈ Z;
x ≥
0, y ≥
0
Так будет удобно и самому школьнику. Пирожные удобнее покупать целыми, чем к примеру несколько целых пирожных и половину пирожного. Кофе также удобнее брать целыми чашками, чем к примеру несколько целых чашек и половину чашки.
Заметим, что при нечетном x невозможно достичь равенства ни при каком y . Тогда значениями x будут следующие числа 0, 2, 4, 6, 8. А зная x можно без труда определить y
Таким образом, мы получили следующие пары значений (0; 20), (2; 15), (4; 10), (6; 5), (8; 0). Эти пары являются решениями или корнями уравнения 25x + 10y = 200 .Они обращают данное уравнение в тождество.
Уравнение вида ax + by = c называют линейным уравнением с двумя переменными . Решением или корнями этого уравнения называют пару значений (x; y ), которая обращает его в тождество.
Отметим также, что если линейное уравнение с двумя переменными записано в виде ax + b y = c , то говорят, что оно записано в каноническом (нормальном) виде.
Некоторые линейные уравнения с двумя переменными могут быть приведены к каноническому виду.
Например, уравнение 2(16x + 3y − 4) = 2(12 + 8x − y ) можно привести к виду ax + by = c . Раскроем скобки в обеих частях этого уравнения, получим 32x + 6y − 8 = 24 + 16x − 2y . Слагаемые, содержащие неизвестные сгруппируем в левой части уравнения, а слагаемые свободные от неизвестных — в правой. Тогда получим 32x − 16x + 6y + 2y = 24 + 8 . Приведём подобные слагаемые в обеих частях, получим уравнение 16x + 8y = 32. Это уравнение приведено к виду ax + by = c и является каноническим.
Рассмотренное ранее уравнение 25x + 10y = 200 также является линейным уравнением с двумя переменными в каноническом виде. В этом уравнении параметры a , b и c равны значениям 25, 10 и 200 соответственно.
На самом деле уравнение ax + by = c имеет бесчисленное множество решений. Решая уравнение 25x + 10y = 200, мы искали его корни толькона множестве целых чисел. В результате получили несколько пар значений, которые обращали данное уравнение в тождество. Но на множестве рациональных чисел уравнение 25x + 10y = 200 будет иметь бесчисленное множество решений.
Для получения новых пар значений, нужно взять произвольное значение для x , затем выразить y . К примеру, возьмем для переменной x значение 7. Тогда получим уравнение с одной переменной 25 × 7 + 10y = 200 в котором можно выразить y
Пусть x = 15 . Тогда уравнение 25x + 10y = 200 примет вид 25 × 15 + 10y = 200. Отсюда находим, что y = −17,5
Пусть x = −3 . Тогда уравнение 25x + 10y = 200 примет вид 25 × (−3) + 10y = 200. Отсюда находим, что y = −27,5
Для уравнения ax + by = c можно сколько угодно раз брать произвольные значение для x и находить значения для y . Отдельно взятое такое уравнение будет иметь бесчисленное множество решений.
Но бывает и так, что переменные x и y связаны не одним, а двумя уравнениями. В этом случае они образуют так называемую систему линейных уравнений с двумя переменными . Такая система уравнений может иметь одну пару значений (или по-другому: «одно решение»).
Может случиться и так, что система вовсе не имеет решений. Бесчисленное множество решений система линейных уравнений может иметь в редких и в исключительных случаях.
Два линейных уравнения образуют систему тогда, когда значения x и y входят в каждое из этих уравнений.
Вернемся к самому первому уравнению 25x + 10y = 200 . Одной из пар значений для этого уравнения была пара (6; 5) . Это случай, когда на 200 рублей можно можно было купить 6 пирожных и 5 чашек кофе.
Составим задачу так, чтобы пара (6; 5) стала единственным решением для уравнения 25x + 10y = 200 . Для этого составим ещё одно уравнение, которое связывало бы те же x пирожных и y чашечек кофе.
Поставим текст задачи следующим образом:
«Школьник купил на 200 рублей несколько пирожных и несколько чашек кофе. Пирожное стоит 25 рублей, а чашка кофе 10 рублей. Сколько пирожных и чашек кофе купил школьник, если известно что количество пирожных на одну единицу больше количества чашек кофе?»
Первое уравнение у нас уже есть. Это уравнение 25x + 10y = 200 . Теперь составим уравнение к условию «количество пирожных на одну единицу больше количества чашек кофе» .
Количество пирожных это x , а количество чашек кофе это y . Можно записать эту фразу с помощью уравнения x − y = 1. Это уравнение будет означать, что разница между пирожными и кофе составляет 1.
x = y + 1 . Это уравнение означает, что количество пирожных на единицу больше, чем количество чашек кофе. Поэтому для получения равенства, к количеству чашек кофе прибавлена единица. Это легко можно понять, если воспользоваться моделью весов, которые мы рассматривали при изучении простейших задач:
Получили два уравнения: 25x + 10y = 200 и x = y + 1. Поскольку значения x и y , а именно 6 и 5 входят в каждое из этих уравнений, то вместе они образуют систему. Запишем эту систему. Если уравнения образуют систему, то они обрамляются знаком системы. Знак системы это фигурная скобка:
Давайте решим данную систему. Это позволит увидеть, как мы придём к значениям 6 и 5. Существует много методов решения таких систем. Рассмотрим наиболее популярные из них.
Название этого метода говорит само за себя. Суть его заключается в том, чтобы одно уравнение подставить в другое, предварительно выразив одну из переменных.
В нашей системе ничего выражать не нужно. Во втором уравнении x = y + 1 переменная x уже выражена. Эта переменная равна выражению y + 1 . Тогда можно подставить это выражение в первое уравнение вместо переменной x
После подстановки выражения y + 1 в первое уравнение вместо x , получим уравнение 25(y + 1) + 10y = 200 . Это линейное уравнение с одной переменной. Такое уравнение решить довольно просто:
Мы нашли значение переменной y . Теперь подставим это значение в одно из уравнений и найдём значение x . Для этого удобно использовать второе уравнение x = y + 1 . В него и подставим значение y
Значит пара (6; 5) является решением системы уравнений, как мы и задумывали. Выполняем проверку и убеждаемся, что пара (6; 5) удовлетворяет системе:
Пример 2
Подставим первое уравнение x = 2 + y во второе уравнение 3x − 2y = 9 . В первом уравнении переменная x равна выражению 2 + y . Это выражение и подставим во второе уравнение вместо x
Теперь найдём значение x . Для этого подставим значение y в первое уравнение x = 2 + y
Значит решением системы является пара значение (5; 3)
Пример 3 . Решить методом подстановки следующую систему уравнений:
Здесь в отличие от предыдущих примеров, одна из переменных не выражена явно.
Чтобы подставить одно уравнение в другое, сначала нужно .
Выражать желательно ту переменную, которая имеет коэффициент единицу. Коэффициент единицу имеет переменная x , которая содержится в первом уравнении x + 2y = 11 . Эту переменную и выразим.
После выражения переменной x , наша система примет следующий вид:
Теперь подставим первое уравнение во второе и найдем значение y
Подставим y x
Значит решением системы является пара значений (3; 4)
Конечно, выражать можно и переменную y . Корни от этого не изменятся. Но если выразить y, получится не очень-то и простое уравнение, на решение которого уйдет больше времени. Выглядеть это будет следующим образом:
Видим, что в данном примере выражать x намного удобнее, чем выражать y .
Пример 4 . Решить методом подстановки следующую систему уравнений:
Выразим в первом уравнении x . Тогда система примет вид:
y
Подставим y в первое уравнение и найдём x . Можно воспользоваться изначальным уравнением 7x + 9y = 8 , либо воспользоваться уравнением , в котором выражена переменная x . Этим уравнением и воспользуемся, поскольку это удобно:
Значит решением системы является пара значений (5; −3)
Метод сложения заключается в том, чтобы почленно сложить уравнения, входящие в систему. Это сложение приводит к тому, что образуется новое уравнение с одной переменной. А решить такое уравнение довольно просто.
Решим следующую систему уравнений:
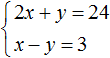
Сложим левую часть первого уравнения с левой частью второго уравнения. А правую часть первого уравнения с правой частью второго уравнения. Получим следующее равенство:
Приведем подобные слагаемые:
В результате получили простейшее уравнение 3x = 27 корень которого равен 9. Зная значение x можно найти значение y . Подставим значение x во второе уравнение x − y = 3 . Получим 9 − y = 3 . Отсюда y = 6 .
Значит решением системы является пара значений (9; 6)
Пример 2
Сложим левую часть первого уравнения с левой частью второго уравнения. А правую часть первого уравнения с правой частью второго уравнения. В получившемся равенстве приведем подобные слагаемые:
В результате получили простейшее уравнение 5x = 20, корень которого равен 4. Зная значение x можно найти значение y . Подставим значение x в первое уравнение 2x + y = 11 . Получим 8 + y = 11 . Отсюда y = 3 .
Значит решением системы является пара значений (4;3)
Процесс сложения подробно не расписывают. Его нужно выполнять в уме. При сложении оба уравнения должны быть приведены к каноническому виду. То есть, к виду ac + by = c .
Из рассмотренных примеров видно, что основная цель сложения уравнений это избавление от одной из переменных. Но не всегда удаётся сразу решить систему уравнений методом сложения. Чаще всего систему предварительно приводят к виду, при котором можно сложить уравнения, входящие в эту систему.
Например, систему 
можно сразу решить методом сложения. При сложении обоих уравнений, слагаемые y
и −y
исчезнут, поскольку их сумма равна нулю. В результате образуется простейшее уравнение 11x
= 22
, корень которого равен 2. Затем можно будет определить y
равный 5.
А систему уравнений 
методом сложения сразу решить нельзя, поскольку это не приведёт к исчезновению одной из переменных. Сложение приведет к тому, что образуется уравнение 8x
+ y
= 28
, имеющее бесчисленное множество решений.
Если обе части уравнения умножить или разделить на одно и то же число, не равное нулю, то получится уравнение равносильное данному. Это правило справедливо и для системы линейных уравнений с двумя переменными. Одно из уравнений (или оба уравнения) можно умножить на какое-нибудь число. В результате получится равносильная система, корни которой будут совпадать с предыдущей.
Вернемся к самой первой системе , которая описывала сколько пирожных и чашек кофе купил школьник. Решением этой системы являлась пара значений (6; 5) .
Умножим оба уравнения, входящие в эту систему на какие-нибудь числа. Скажем первое уравнение умножим на 2, а второе на 3
В результате получили систему 
Решением этой системы по-прежнему является пара значений (6; 5)
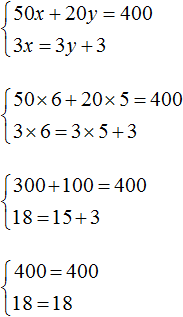
Это значит, что уравнения входящие в систему можно привести к виду, пригодному для применения метода сложения.
Вернемся к системе , которую мы не смогли решить методом сложения.
Умножим первое уравнение на 6, а второе на −2
Тогда получим следующую систему:
Сложим уравнения, входящие в эту систему. Сложение компонентов 12x и −12x даст в результате 0, сложение 18y и 4y даст 22y , а сложение 108 и −20 даст 88. Тогда получится уравнение 22y = 88 , отсюда y = 4 .
Если первое время тяжело складывать уравнения в уме, то можно записывать как складывается левая часть первого уравнения с левой частью второго уравнения, а правая часть первого уравнения с правой частью второго уравнения:
Зная, что значение переменной y равно 4, можно найти значение x . Подставим y в одно из уравнений, например в первое уравнение 2x + 3y = 18 . Тогда получим уравнение с одной переменной 2x + 12 = 18 . Перенесем 12 в правую часть, изменив знак, получим 2x = 6 , отсюда x = 3 .
Пример 4 . Решить следующую систему уравнений методом сложения:
Умножим второе уравнение на −1. Тогда система примет следующий вид:
Сложим оба уравнения. Сложение компонентов x и −x даст в результате 0, сложение 5y и 3y даст 8y , а сложение 7 и 1 даст 8. В результате получится уравнение 8y = 8 , корень которого равен 1. Зная, что значение y равно 1, можно найти значение x .
Подставим y в первое уравнение, получим x + 5 = 7 , отсюда x = 2
Пример 5 . Решить следующую систему уравнений методом сложения:
Желательно, чтобы слагаемые содержащие одинаковые переменные, располагались друг под другом. Поэтому во втором уравнении слагаемые 5y и −2x поменяем местами. В результате система примет вид:
Умножим второе уравнение на 3. Тогда система примет вид:
Теперь сложим оба уравнения. В результате сложения получим уравнение 8y = 16 , корень которого равен 2.
Подставим y в первое уравнение, получим 6x − 14 = 40 . Перенесем слагаемое −14 в правую часть, изменив знак, получим 6x = 54 . Отсюда x = 9.
Пример 6 . Решить следующую систему уравнений методом сложения:
Избавимся от дробей. Умножим первое уравнение на 36, а второе на 12
В получившейся системе 
первое уравнение можно умножить на −5, а второе на 8
Сложим уравнения в получившейся системе. Тогда получим простейшее уравнение −13y = −156 . Отсюда y = 12 . Подставим y в первое уравнение и найдем x
Пример 7 . Решить следующую систему уравнений методом сложения:
Приведем оба уравнения к нормальному виду. Здесь удобно применить правило пропорции в обоих уравнениях. Если в первом уравнении правую часть представить как , а правую часть второго уравнения как , то система примет вид:
У нас получилась пропорция. Перемножим её крайние и средние члены. Тогда система примет вид:
Первое уравнение умножим на −3, а во втором раскроем скобки:
Теперь сложим оба уравнения. В результате сложения этих уравнений, мы получим равенство, в обеих частях которого будет ноль:
Получается, что система имеет бесчисленное множество решений.
Но мы не можем просто так взять с неба произвольные значения для x и y . Мы можем указать одно из значений, а другое определится в зависимости от значения, указанного нами. Например, пусть x = 2 . Подставим это значение в систему:
В результате решения одного из уравнений, определится значение для y , которое будет удовлетворять обоим уравнениям:
Получившаяся пара значений (2; −2) будет удовлетворять системе:
Найдём еще одну пару значений. Пусть x = 4. Подставим это значение в систему:
На глаз можно определить, что значение y равно нулю. Тогда получим пару значений (4; 0), которая удовлетворяет нашей системе:
Пример 8 . Решить следующую систему уравнений методом сложения:
Умножим первое уравнение на 6, а второе на 12
Перепишем то, что осталось:
Первое уравнение умножим на −1. Тогда система примет вид:
Теперь сложим оба уравнения. В результате сложения образуется уравнение 6b = 48 , корень которого равен 8. Подставим b в первое уравнение и найдём a
В линейное уравнение с тремя переменными входит три переменные с коэффициентами, а также свободный член. В каноническом виде его можно записать следующим образом:
ax + by + cz = d
Данное уравнение имеет бесчисленное множество решений. Придавая двум переменным различные значения, можно найти третье значение. Решением в этом случае является тройка значений (x; y; z ) которая обращает уравнение в тождество.
Если переменные x, y, z связаны между собой тремя уравнениями, то образуется система трех линейных уравнений с тремя переменными. Для решения такой системы можно применять те же методы, которые применяются к линейным уравнениям с двумя переменными: метод подстановки и метод сложения.
Пример 1 . Решить следующую систему уравнений методом подстановки:
Выразим в третьем уравнении x . Тогда система примет вид:
Теперь выполним подстановку. Переменная x равна выражению 3 − 2y − 2z . Подставим это выражение в первое и второе уравнение:
Раскроем скобки в обоих уравнениях и приведём подобные слагаемые:
Мы пришли к системе линейных уравнений с двумя переменными. В данном случае удобно применить метод сложения. В результате переменная y исчезнет, и мы сможем найти значение переменной z
Теперь найдём значение y . Для этого удобно воспользоваться уравнением −y + z = 4. Подставим в него значение z
Теперь найдём значение x . Для этого удобно воспользоваться уравнением x = 3 − 2y − 2z . Подставим в него значения y и z
Таким образом, тройка значений (3; −2; 2) является решением нашей системы. Проверкой убеждаемся, что эти значения удовлетворяют системе:
Пример 2 . Решить систему методом сложения
Сложим первое уравнение со вторым, умноженным на −2.
Если второе уравнение умножить на −2, то оно примет вид −6x + 6y − 4z = −4 . Теперь сложим его с первым уравнением:
Видим, что в результате элементарных преобразований, определилось значение переменной x . Оно равно единице.
Вернемся к главной системе. Сложим второе уравнение с третьим, умноженным на −1. Если третье уравнение умножить на −1, то оно примет вид −4x + 5y − 2z = −1 . Теперь сложим его со вторым уравнением:
Получили уравнение x − 2y = −1 . Подставим в него значение x , которое мы находили ранее. Тогда мы сможем определить значение y
Теперь нам известны значения x и y . Это позволяет определить значение z . Воспользуемся одним из уравнений, входящим в систему:
Таким образом, тройка значений (1; 1; 1) является решением нашей системы. Проверкой убеждаемся, что эти значения удовлетворяют системе:
Задача на составление систем уравнений решается путем ввода нескольких переменных. Далее составляются уравнения на основании условий задачи. Из составленных уравнений образуют систему и решают её. Решив систему, необходимо выполнить проверку на то, удовлетворяет ли её решение условиям задачи.
Задача 1 . Из города в колхоз выехала машина «Волга». Обратно она возвращалась по другой дороге, которая была на 5 км короче первой. Всего в оба конца машина проехала 35 км. Сколько километров составляет длина каждой дороги?
Решение
Пусть x — длина первой дороги, y — длина второй. Если в оба конца машина проехала 35 км, то первое уравнение можно записать как x + y = 35. Это уравнение описывает сумму длин обеих дорог.
Сказано, что обратно машина возвращалась по дороге которая была короче первой на 5 км. Тогда второе уравнение можно записать как x − y = 5. Это уравнение показывает, что разница между длинами дорог составляет 5 км.
Либо второе уравнение можно записать как x = y + 5 . Этим уравнением и воспользуемся.
Поскольку переменные x и y в обоих уравнениях обозначают одно и то же число, то мы можем образовать из них систему:
Решим эту систему каким-нибудь из изученных ранее методов. В данном случае удобно воспользоваться методом подстановки, поскольку во втором уравнении переменная x уже выражена.
Подставим второе уравнение в первое и найдём y
Подставим найденное значение y в во второе уравнение x = y + 5 и найдём x
Длина первой дороги была обозначена через переменную x . Теперь мы нашли её значение. Переменная x равна 20. Значит длина первой дороги составляет 20 км.
А длина второй дороги была обозначена через y . Значение этой переменной равно 15. Значит длина второй дороги составляет 15 км.
Выполним проверку. Для начала убедимся, что система решена правильно:
Теперь проверим удовлетворяет ли решение (20; 15) условиям задачи.
Было сказано, что всего в оба конца машина проехала 35 км. Складываем длины обеих дорог и убеждаемся, что решение (20; 15) удовлетворяет данному условию: 20 км + 15 км = 35 км
Следующее условие: обратно машина возвращалась по другой дороге, которая была на 5 км короче первой . Видим, что решение (20; 15) удовлетворяет и этому условию, поскольку 15 км короче, чем 20 км на 5 км: 20 км − 15 км = 5 км
При составлении системы важно, чтобы переменные обозначали одни и те же числа во всех уравнениях, входящих в эту систему.
Так наша система содержит два уравнения. Эти уравнения в свою очередь содержат переменные x и y , которые обозначают одни и те же числа в обоих уравнениях, а именно длины дорог, равных 20 км и 15 км.
Задача 2 . На платформу были погружены дубовые и сосновые шпалы, всего 300 шпал. Известно, что все дубовые шпалы весили на 1 т меньше, чем все сосновые. Определить, сколько было дубовых и сосновых шпал отдельно, если каждая дубовая шпала весила 46 кг, а каждая сосновая 28 кг.
Решение
Пусть x дубовых и y сосновых шпал было погружено на платформу. Если всего шпал было 300, то первое уравнение можно записать как x + y = 300 .
Все дубовые шпалы весили 46x кг, а сосновые весили 28y кг. Поскольку дубовые шпалы весили на 1 т меньше, чем сосновые, то второе уравнение можно записать, как 28y − 46x = 1000 . Это уравнение показывает, что разница масс между дубовыми и сосновыми шпалами, составляет 1000 кг.
Тонны были переведены в килограммы, поскольку масса дубовых и сосновых шпал измерена в килограммах.
В результате получаем два уравнения, которые образуют систему
Решим данную систему. Выразим в первом уравнении x . Тогда система примет вид:
Подставим первое уравнение во второе и найдём y
Подставим y в уравнение x = 300 − y и узнаем чему равно x
Значит на платформу было погружено 100 дубовых и 200 сосновых шпал.
Проверим удовлетворяет ли решение (100; 200) условиям задачи. Для начала убедимся, что система решена правильно:
Было сказано, что всего было 300 шпал. Складываем количество дубовых и сосновых шпал и убеждаемся, что решение (100; 200) удовлетворяет данному условию: 100 + 200 = 300.
Следующее условие: все дубовые шпалы весили на 1 т меньше, чем все сосновые . Видим, что решение (100; 200) удовлетворяет и этому условию, поскольку 46 × 100 кг дубовых шпал легче, чем 28 × 200 кг сосновых шпал: 5600 кг − 4600 кг = 1000 кг.
Задача 3 . Взяли три куска сплава меди с никелем в отношениях 2: 1 , 3: 1 и 5: 1 по массе. Из них сплавлен кусок массой 12 кг с отношением содержания меди и никеля 4: 1 . Найдите массу каждого исходного куска, если масса первого из них вдвое больше массы второго.
