Литература: [Л.1], с 40
В качестве примера приведем разложение в ряд Фурье периодической последовательности прямоугольных импульсов с амплитудой , длительностью и периодом следования , симметричной относительно нуля, т.е.
, (2.10)
Здесь 
Разложение такого сигнала в ряд Фурье дает
, (2.11)
где – скважность.
Для упрощения записи можно ввести обозначение
, (2.12)
Тогда (2.11) запишется следующим образом
, (2.13)
На рис. 2.3 изображена последовательность прямоугольных импульсов. Спектр последовательности, как впрочем, и любого другого периодического сигнала, носит дискретный (линейчатый) характер.
Огибающая спектра (рис. 2.3, б) пропорциональна 
. Расстояние по оси частот между двумя соседними составляющими спектра равно , а между двумя нулевыми значениями (ширина лепестка спектра) – . Число гармонических составляющих в пределах одного лепестка, включая правое по рисунку нулевое значение, составляет , где знак означает округление до ближайшего целого числа, меньшего (если скважность – дробное число), или (при целочисленном значении скважности). При увеличении периода основная частота 
уменьшается, спектральные составляющие на диаграмме сближаются, амплитуды гармоник также уменьшаются. При этом форма огибающей сохраняется.
При решении практических задач спектрального анализа вместо угловых частот используют циклические частоты 
, измеряемые в Герцах. Очевидно, расстояние между соседними гармониками на диаграмме составит , а ширина одного лепестка спектра – . Эти значения представлены на диаграмме в круглых скобках.
В практической радиотехнике в большинстве случаев вместо спектрального представления (рис. 2.3, б) используют спектральные диаграммы амплитудного и фазового спектров. Амплитудный спектр последовательности прямоугольных импульсов представлен на рис. 2.3, в.
Очевидно, огибающая амплитудного спектра пропорциональна 
.
Что же касается фазового спектра (рис. 2.3, г), то полагают, что начальные фазы гармонических составляющих изменяются скачком на величину -π при изменение знака огибающей sinc kπ/q . Начальные фазы гармоник первого лепестка, полагаются равными нулю. Тогда начальные фазы гармоник второго лепестка составят φ = -π , третьего лепестка φ = -2π и т.д.
Рассмотрим еще одно представление сигнала рядом Фурье. Для этого воспользуемся формулой Эйлера
.
В соответствии с этой формулой k-ю составляющую (2.9) разложения сигнала в ряд Фурье можно представить следующим образом
; 
. (2.15)
Здесь величины и являются комплексными и представляют собой комплексные амплитуды составляющих спектра. Тогда ряд
Фурье (2.8) с учетом (2.14) примет следующую форму
, (2.16)
, (2.17)
Нетрудно убедиться в том, что разложение (2.16) проводится по базисным функциям 
, которые также являются ортогональными на интервале 
, т.е.
Выражение (2.16) представляет собой комплексную форму
ряда Фурье, которая распространяется на отрицательные частоты. Величины и 
, где означает комплексную сопряженную с величину, называются комплексными амплитудами
спектра. Т.к. является комплексной величиной, из (2.15) следует, что
и 
.
Тогда совокупность составляет амплитудный, а совокупность – фазовый спектр сигнала .
На рис. 2.4 представлена спектральная диаграмма спектра рассмотренной выше последовательности прямоугольных импульсов, представленного комплексным рядом Фурье
Спектр также носит линейчатый характер, но в отличие от ранее рассмотренных спектров определяется как в области положительных, так и в области отрицательных частот. Поскольку является чётной функцией аргумента , спектральная диаграмма симметрична относительно нуля.
Исходя из (2.15) можно установить соответствие между и коэффициентами и разложения (2.3). Так как
и 
,
то в результате получим
. (2.18)
Выражения (2.5) и (2.18) позволяют найти значения при практических расчетах.
Дадим геометрическую интерпретацию комплексной формы ряда Фурье. Выделим k-тую составляющую спектра сигнала. В комплексной форме k-я составляющая описывается формулой
где и определятся выражениями (2.15).
В комплексной плоскости каждое из слагаемых в (2.19) изображается в виде векторов длиной 
, повернутых на угол и относительно вещественной оси и вращающихся в противоположных направлениях с частотой (рис. 2.5).
Очевидно, сумма этих векторов дает вектор, расположенный на вещественной оси, длина которого составляет . Но этот вектор соответствует гармонической составляющей
Что касается проекций векторов на мнимую ось, то эти проекции имеют равную длину, но противоположные направления и в сумме дают ноль. А это значит, что сигналы, представленные в комплексной форме (2.16) в действительности являются вещественными сигналами. Иными словами, комплексная форма ряда Фурье является математической абстракцией, весьма удобной при решении целого ряда задач спектрального анализа. Поэтому, иногда спектр, определяемый тригонометрическим рядом Фурье, называют физическим спектром , а комплексной формой ряда Фурье – математическим спектром .
И в заключение рассмотрим вопрос распределения энергии и мощности в спектре периодического сигнала. Для этого воспользуемся равенством Парсеваля (1.42). При разложении сигнала в тригонометрический ряд Фурье выражение (1.42) принимает вид
.
Энергия постоянной составляющей
,
а энергия k-той гармоники
.
Тогда энергия сигнала
. (2.20)
Т.к. средняя мощность сигнала
,
то с учетом (2.18)
. (2.21)
При разложение сигнала в комплексный ряд Фурье выражение (1.42) имеет вид
,
где 
- энергия k-той гармоники.
Энергия сигнала в этом случае
,
а его средняя мощность
.
Из приведенных выражений следует, что энергия или средняя мощность k-той спектральной составляющей математического спектра вдвое меньше энергии или мощности соответствующей спектральной составляющей физического спектра. Это обусловлено тем, что физического спектра распределяется поровну между и математического спектра.
| -τ и /2 |
| τ и /2 |
| Т |
| t |
| U 0 |
| S(t) |
СИГНАЛОВ
Рассмотрим несколько примеров периодических колебаний, часто используемых в различных радиотехнических устройствах.
Подобное колебание, часто называемое меандром, находит особенно широкое применение в измерительной технике.
При выборе начала отсчета времени в соответствии с рис. 2.3, а функция является нечетной, а рис. 2.3, б - четной. Применяя формулы (2.24), находим для нечетной функции (рис. 2.3, а) при s(t)=e(t):
Рис. 2.3. Периодическое колебание прямоугольной формы (меандр)
Рис. 2.4. Коэффициенты комплексного (а) и тригонометрического (б) ряда Фурье колебания, показанного на рис. 2.3
Учитывая, что , получаем
Начальные фазы в соответствии с (2.27) равны для всех гармоник.
Запишем ряд Фурье в тригонометрической форме
Спектр коэффициентов комплексного ряда Фурье показан на рис. 2.4, а, а тригонометрического ряда - на рис. 2.4, б (при ).
При отсчете времени от середины импульса (рис. 2.3, б) функция является четной относительно t и для нее
Графики 1-й гармоник и их суммы изображены на рис. 2.5, а. На рис. 2.5, б эта сумма дополнена 5-й гармоникой, а на рис. 2.5, в - 7-й.
С увеличением числа суммируемых гармоник сумма ряда приближается к функции всюду, кроме точек разрыва функции, где образуется выброс. При величина этого выброса равна , т. е. сумма ряда отличается от заданной функции на 18%. Этот дефект сходимости в математике получил название явления Гиббса.
Рис. 2.5. Суммирование 1-й и 3-й гармоник (а), 1, 3 и 5-й гармоник (б), 1, 3, 5 и 7-й гармоник (в) колебания, показанного на рис. 2.3
Рис. 2.6 Периодическое колебание пилообразной формы
Рис. 2.7. Сумма первых пяти гармоник колебания, показанного на рис. 2.6
Несмотря на то, что в рассматриваемом случае ряд Фурье не сходится к разлагаемой функции в точках ее разрыва, ряд сходится в среднем, поскольку при выбросы являются бесконечно узкими и не вносят никакого вклада в интеграл (2.13).
С подобными функциями часто приходится иметь дело в устройствах для развертки изображения в осциллографах. Так как эта функция является нечетной, ряд Фурье для нее содержит только синусоидальные члены. С помощью формул (2.24)-(2.31) нетрудно определить коэффициенты ряда Фурье. Опуская эти выкладки, напишем окончательное выражение для ряда
Как видим, амплитуды гармоник убывают по закону , где . На рис. 2.7 показан график суммы первых пяти гармоник (в увеличенном масштабе).
Ряд Фурье для этой функции имеет следующий вид:
Рис. 2.8. Сумма трех первых гармоник периодической функции
Рис. 2.9. Периодическая последовательность прямоугольных импульсов с большой скважностью
На рис. 2.8 изображена сумма первых трех членов этого ряда. В данном случае отметим более быстрое убывание амплитуд гармоник, чем в предыдущих примерах. Это объясняется отсутствием разрывов (скачков) в функции.
Применяя формулу (2.32), находим среднее значение (постоянную составляющую)
и коэффициент гармоники
Спектральное представление временных функций широко используется в теории связи. Для теоретических и экспериментальных исследований характеристик электрических цепей и передачи сообщений по каналам связи используется различные типы сигналов: гармонические колебания, уровни постоянных напряжений, последовательности прямоугольных и радиоимпульсов и т. д. Особо важную роль в теоретических исследованиях электрических цепей играют вычислительные сигналы в форме единичной функции и импульсной функции (функции Дирака). Определим спектры наиболее распространенных типовых сигналов.
11.1 Спектр последовательности прямоугольных импульсов
Пусть имеется периодическая последовательность импульсов прямоугольной формы периодом Т длительностью импульсов t и и амплитудой А. Аналитическое выражение функции , описывающей импульс на отрезке , имеет вид
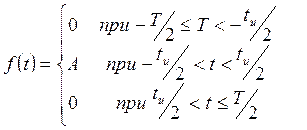(11.1)
График периодической последовательности импульсов изображен на рисунке 11.1.
Рисунок 11.1
Данная функция является четной, так как ее график симметричен относительно оси ординат. Тогда коэффициенты Фурье это функции вычисляются по формулам (КФТ2), где .
Число представляет собой среднее значение функции за период и называется постоянной составляющей. Частоту называют основной, или первой гармоникой, а частоты k высшими гармониками, где k=2,3,4,…
Построим амплитудный спектр рассматриваемой последовательности прямоугольных импульсов. Так как функция периодическая, то ее амплитудный спектр является линейчатым. Обозначим через расстояние между любыми соседними гармониками. Очевидно, оно равно . Амплитуда k-ой гармоники согласно (11.2) имеет вид
(11.3)
Найдем отношение между периодом Т и длительностью импульса , при котором амплитуда k-ой гармоники обращается в нуль.
А 2 ≈32В, А 3 ≈15В, А 4 ≈0, А 5 ≈6,36В, А 6 ≈10,5В, А 7 ≈6,36В, А 8 ≈0, А 9 ≈4,95В, А 10 ≈6,37В.
Полученный в результате расчета амплитудный спектр приведен на рисунке 11.2.
Рисунок 11.2
Такой спектр называют линейчатым или дискретным спектром.
Аналогично рассчитаны и построены спектры для q=8 и q=16. Они приведены на рисунках 11.3 и 11.4 соответственно.
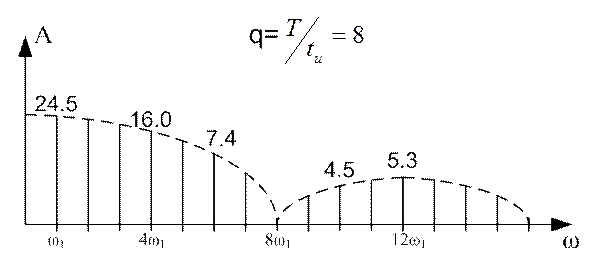
Рисунок 11.3
Рисунок 11.4
Из рисунка видно, что чем больше скважность прямоугольных импульсов, тем меньше значение имеет амплитуда первой гармоники, но тем медленнее убывает спектр.
11.2 Спектр одиночного прямоугольного импульса
Рассмотрим Ф (11.1) для случая, когда Т→∞, то есть периодическая последовательность импульсов вырождается в одиночный прямоугольный импульс, длительностью t u .
Аналитическое выражение для этого импульса запишется в виде:
График этой функции изображен на рисунке 11.5.
Рисунок 11.5
В этом случае частота первой гармоники и расстояние между гармониками становится равным 0, следовательно, спектр из дискретного превращается в непрерывный, состоящий из бесконечно большого числа спектральных линий, находящихся на бесконечно малых расстояниях друг от друга. Такой спектр называют сплошным. Отсюда следует важнейшее правило: периодические сигналы порождают дискретные спектры, а непериодические – сплошные (непрерывные).
Спектр прямоугольного одиночного импульса можно найти непосредственно из прямого преобразования Фурье (10.1)
С выхода источника сообщений поступают сигналы, несущие информацию, а также тактовые, используемые для синхронизации работы передатчика и приемника системы передачи. Информационные сигналы имеют вид непериодической, а тактовые- периодическойпоследовательности импульсов.
Для правильной оценки возможности передачи таких импульсов по каналам связи определим их спектральный состав. Периодический сигнал в виде импульсов любой формы можно разложить в ряд Фурье согласно (7).
Для передачи по воздушным и кабельным линиям связи применяются сигналы различной формы. Выбор той или иной формы зависит от характера передаваемых сообщений, частотного спектра сигналов, частотных ивременных параметров сигналов. Большое применение в технике передачи дискретных сообщений получили сигналы, близкие по форме к прямоугольным импульсам.
Вычислим спектр, т.е. совокупность амплитуд постоянной и
гармонических составляющих периодических
прямоугольных импульсов (рисунок 4,а)
длительностью
и периодом.
Поскольку сигнал является четной
функцией времени, то в выражении (3) все
четные гармонические составляющие
обращаются в нуль (
=0),
а нечетные составляющие принимают
значения:
(10)
Постоянная составляющая равна
(11)
Для сигнала 1:1 (телеграфные точки) рисунок 4а:
,
.
(12)
Модули амплитуд спектральных составляющих
последовательности прямоугольных
импульсов с периодом
приведены на рис. 4,б. По оси абсцисс
отложены основная частота повторения
импульсов
()
и частоты нечетных гармонических
составляющих
,
и т.д. Огибающая спектра изменяется по
закону.
При увеличении периода ,по сравнению с длительностью импульса,число гармонических составляющих в спектральном составе периодического сигнала увеличиваются. Например, для сигнала с периодом (рисунок 4,в)получаем, что постоянная составляющая равнаи
В полосе частот от нуля до частотырасполагается пять гармоническихсоставляющих (рисунок 4,г), в то время как прилишь одна.
При дальнейшем
увеличении периода повторения импульсов
число гармонических составляющих
становится все больше и больше. В
предельном случае когда
сигнал становится непериодической
функцией времени, число его гармонических
составляющих в полосе частот от нуля
до частотыувеличивается
до бесконечности; расположены они будут
набесконечноблизких
расстояниях по частоте;спектр непериодического
сигналастановится
непрерывным.
Рисунок 4
Задан одиночный видеоимпульс (рисунок 5):
Рисунок 5
Метод рядов Фурье допускает глубокое и плодотворное обобщение, позволяющее получать спектральные характеристики непериодических сигналов. Для этого мысленно дополним одиночный импульс такими же импульсами, периодически следующими через некоторый интервал времени , и получим изученную ранее периодическую последовательность:
Представим одиночный импульс как сумму периодических импульсов с большим периодом .
,
(14)
где - целые числа.
Для периодического колебания
.
(15)
Для того, чтобы вернуться к одиночному импульсу, устремим к бесконечности период повторения: . При этом, очевидно:
,
(16)
Обозначим
.
(17)
Величиной называется спектральная характеристика (функция) одиночного импульса (прямое преобразование Фурье). Она зависит только от временного описания импульсаи в общем виде является комплексной:
,
(18) где
; (19)
; (20)
,
где
-
модуль спектральной функции
(амплитудно-частотная характеристика
импульса);
-
фазовый угол, фазо-частотная характеристика
импульса.
Найдем для одиночного импульса по формуле (8), используя спектральную функцию:
.
Если , получим:
.
(21)
Полученное выражение называется обратным преобразованием Фурье.
Интеграл Фурье определяет импульс в виде бесконечной суммы бесконечно малых гармонических составляющих, расположенных на всех частотах.
На этом основании говорят о непрерывном (сплошном) спектре, которым обладает одиночный импульс.
Полная энергия импульса (энергия, выделяемая на активном сопротивлении Ом) равна
(22)
Изменяя порядок интегрирования, получим
.
Внутренний интеграл есть спектральная
функция импульса
,
взятая при аргументе -,
т.е. представляет собой комплексно
сопряженную свеличину:
Следовательно
Квадрат модуля (произведение двух сопряженных комплексных чисел равно квадрату модуля).
В этом случае условно говорят, что спектр импульса является двусторонним, т.е. размещается в полосе частот от до.
Приведенное соотношение (23), устанавливающее связь между энергией импульса (на сопротивлении 1 Ом) и модулем его спектральной функции известно под названием равенство Парсеваля.
Оно утверждает, что энергия, заключенная в импульсе , равна сумме энергий всех составляющих его спектра. Равенство Парсеваля характеризует важное свойство сигналов. Если некоторая избирательная система пропускает только часть спектра сигнала, ослабляя другие её составляющие, то это означает, что часть энергии сигнала теряется.
Так как квадрат модуля является четной функцией переменной интегрирования , то удвоив значение интеграла можно ввести интегрирование в пределах от 0 до:
.
(24)
При этом говорят, что спектр импульса размещается в полосе частот от 0 до и называется односторонним.
Подынтегральная величина в (23) называется энергетическим спектром (спектральная плотность энергии) импульса
Она характеризует распределение энергии по частоте, и её значение на частоте равно энергии импульса, приходящейся на полосу частот, равной 1 Гц. Следовательно, энергия импульса есть результат интегрирования энергетического спектра сигнала по всему диапазону частот отдо.Иначе говоря, энергия равна площади, заключённой между кривой, изображающей энергетический спектр сигнала и осью абсцисс.
Для оценки распределения энергии по спектру пользуются относительной интегральной функцией распределения энергии (энергетической характеристикой)
,
(25)
где
-
энергия импульса в заданной полосе
частот от 0 до,
которая характеризует долю энергии
импульса, сосредоточенную в интервале
частот от 0 до.
Для одиночных импульсов различной формы выполняются следующие закономерности:
Лабораторная работа №1.
Представление периодических импульсных
Сигналов рядом Фурье.
Цель работы – Изучение спектрального состава периодической последовательности импульсов прямоугольной формы при различных частотах следования и длительности импульсов.
Введение
Для, передачи хранения и обработки информации используются периодические импульсные сигналы, которые могут быть математически представлены рядами Фурье. Существует временное рис.1 и частотное представление электрических сигналов рис.2.
Рис.1. Временная форма представления периодической
последовательности прямоугольных импульсов.
Представление сигнала во временной области позволяет определить его параметры, энергию, мощность и длительность. Для представления сигналов в частотной области в виде спектра используется преобразования Фурье. Знание частотных свойств позволяет решать задачи идентификации характеристик сигнала (определение его наиболее информативных параметров), фильтрации (выделение полезного сигнала на фоне помех), выбора частоты дискретизации непрерывного сигнала. Одним из важнейших параметров сигнала является ширина частотного спектра, т. к. именно этот параметр оказывается определяющим при согласовании сигнала с аппаратурой обработки и передачи информации.
Основные формулы и определения.
Периодическую функциюu(t) с периодом T можно представить рядом Фурье
(1)
Колебание 
с частотой называется первой гармоникой; (n =1) колебание 
с частотой - второй гармоникой (n =2), 
c частотой - n-й гармоникой.
Выражение (1) с использованием тождества
может быть переписано в виде
, (2)
Коэффициенты и определяется по формулам
Величина выражает среднее значение функции за период, она, называется также постоянной составляющей и вычисляется по формуле
Формулы (3) решают задачу анализа : по заданной периодической функции нужно найти коэффициенты Фурье и . Формулы (1) и (2) решают задачу гармонического синтеза : по заданным коэффициентам и нужно найти периодическую функцию .
Анализ спектра последовательности прямоугольных импульсов
Совокупность амплитуд и частот гармонических составляющих называютамплитудной-частотной характеристикой
(АЧХ), а зависимость от частот гармоник фазо-частотной характеристикой (ФЧХ).
Амплитудно-частотный спектр прямоугольных импульсов может быть представлен графически рис.2. 
Рис.2. АЧХ и ФЧХ периодической последовательности
прямоугольных импульсов.
Пусть , представляющая последовательность прямоугольных импульсов рис.1 с амплитудой , длительностью и периодом описывается уравнением
Тогда амплитуды и фазы для гармонических составляющих определяются уравнением:
(4)
Величина называется скважностью и обозначается буквой . Тогда уравнения (4) принимают вид
где n =1, 2, … . (5)
Для вычисления мощности сигналов представленных рядом Фурье в теории информации используют формулы в которых значение сопротивление R = 1 Ом. В этом случае напряжения u и токи i равны, поскольку i = u/R.
Мощность постоянной составляющей Р 0 будет
а мощность переменной составляющей Р n для n-й гармоники
(6)
Формула для результирующей мощности примет вид
ЗАДАНИЕ
1. Выполните анализ периодической последовательности прямоугольных импульсов
1.1 По номеру варианта N, полученного у преподавателя, определите из таблицы 1 значение скважности и круговой частоты .
Таблица 1
| №, вар | q | , рад/с | №, вар | q | , рад/с |
| 3,24 | 47,25 | 8,50 | 69,22 | ||
| 6,52 | 97,50 | 6,72 | 78,59 | ||
| 5,93 | 14,45 | 2,30 | 19,44 | ||
| 7,44 | 15,12 | 3,59 | 37,96 | ||
| 1,87 | 70,93 | 4,48 | 78,27 | ||
| 5,46 | 91,65 | 2,99 | 42,48 | ||
| 6,40 | 86,40 | 6,18 | 75,45 | ||
| 1,27 | 48,98 | 1,81 | 57,64 | ||
| 2,97 | 40,13 | 3,22 | 15,46 | ||
| 1,09 | 85,95 | 3,66 | 55,25 | ||
| 2,13 | 57,30 | 3,27 | 27,58 | ||
| 7,99 | 66,90 | 4,64 | 3,68 | ||
| 4,61 | 31,55 | 3,71 | 43,73 | ||
| 1,95 | 25,24 | 4,33 | 70,44 | ||
| 2,66 | 6,61 | 3,38 | 52,07 | ||
| 1,10 | 18,37 | 6,92 | 26,17 | ||
| 4,06 | 70,24 | 4,95 | 55,52 | ||
| 2,40 | 35,10 | 6,51 | 82,64 | ||
| 9,42 | 33,96 | 3,32 | 68,07 | ||
| 6,13 | 43,25 | 7,75 | 32,49 | ||
| 7,36 | 52,37 | 5,71 | 26,68 | ||
| 2,33 | 24,84 | 2,42 | 96,02 | ||
| 2,18 | 25,34 | 16,99 | 88,59 | ||
| 5,80 | 12,99 | 62,23 | 50,21 | ||
| 1,68 | 41,16 | 37,54 | 20,70 |
1.2 а) Определите 11 первых значений коэффициентов u n (n=0, 1, 2, ... , 10), считая Е=1 В, используя электронные таблицы "Exel" (или калькулятор, или другой программный продукт) по формулам (5) и и внесите их в соответствующую строку u n таблицы 2.
1.3 б) Вычислите мощности p n и запишите их в таблицу 2.
Таблица 2
| w | w 1 | 2w 1 | … | 10w 1 | |
| u n | u 0 | u 1 | u 2 | … | u 10 |
| j n | j 1 | j 2 | j 3 | … | j 10 |
| p n | p 0 | p 1 | p 2 | p 10 |
и графика амплитудно-частотной характеристики (АЧХ) рис.3, а).
1.4 Постройте фазо-частотную характеристику (ФЧХ) периодической последовательности импульсов подобно рис.2) в которой изменение знака u n эквивалентно сдвигу фазы на p.
1.5 Вычислите удельную (на сопротивлении 1 Ом) мощность спектра первых 10 гармоник по формуле
.
2. Задача синтеза.
2.1. Используя уравнение (1), представьте сумму первых 10 гармоник подставив в виде уравнения
по вычисленным в таблице значениям u n для , , , …. и постройте временную зависимость на периоде Т, например.
из таблицы 3
в виде графика 4 во временном диапазоне одного периода Т= , используя текущее время t = nD t - t/2, с шагом где n=0,1,2, … ,10 , показанного на рис. 3 .
Рис. 3. Временной интервал для синтеза сигнала
